5 Conclusions

  Overall, the radix-4 implementation executes faster on the platforms tested than the author's radix-2 algorithm. The predicted number of additions and multiplications as reported in section 2 shows that radix-2, as it has been implemented here, requires far fewer multiplications than radix-4. The difference between the number of multiplications required for the author's implementation of radix-2 and radix-4, for a given sequence length, N, is found in equation (15):

 

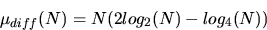$$\mu_{diff}(N) = N ( 2 log_2 (N) - log_4 (N) )$$ (8)

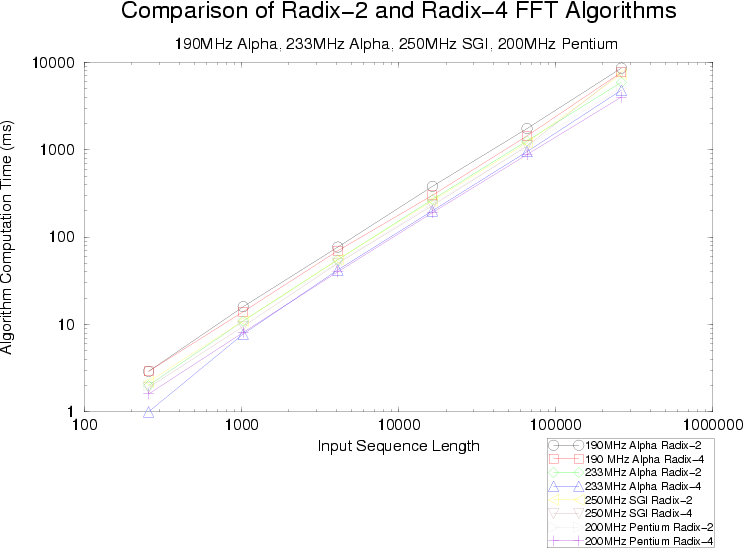
Additionally, the overall computation time is unsurprisingly exponential as a function of sequence length, N; evidenced by the linear traces on the logarithmic plot. Shown in figure 1 are comparison curves for the radix-2 and radix-4 algorithm implementations, plotted on a log-log plot, displaying computation time on the vertical axis and sequence length on the horizontal axis.

  

Figure 1: Comparison of radix-2 and radix-4 FFT algorithms across 4 platforms.